La rotación de un cuerpo se representa mediante un operador que afecta a un conjunto de puntos o vectores. El movimiento rotatorio se representa mediante el vector velocidad angular
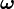 ,
que es un vector de carácter deslizante y situado sobre el eje de
rotación. Cuando el eje pasa por el centro de masa o de gravedad se dice
que el cuerpo «gira sobre sí mismo».
,
que es un vector de carácter deslizante y situado sobre el eje de
rotación. Cuando el eje pasa por el centro de masa o de gravedad se dice
que el cuerpo «gira sobre sí mismo».Concepto de rotación y revolución
- La rotación de un cuerpo alrededor de un eje
(exterior o interior al cuerpo) corresponde a un movimiento en el que
los distintos puntos del cuerpo presentan velocidades que son
proporcionales a su distancia al eje. Los puntos del cuerpo situados
sobre el eje (en el caso de que éste sea interior al cuerpo) permanecen
en reposo.
- La orientación del cuerpo en el espacio cambia continuamente durante la traslación.
- Un ejemplo de rotación es el de la Tierra alrededor de su propio eje de rotación, con un período de rotación de un día sidéreo.
- La revolución de una partícula o de un cuerpo extenso corresponde a un movimiento de traslación del cuerpo alrededor de otro.
- Un ejemplo de revolución es el de la Tierra alrededor del Sol, con un periodo de revolución de un año.
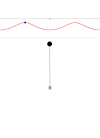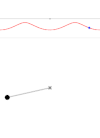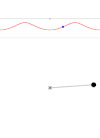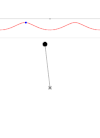
Las trayectorias recorridas por los distintos puntos del cuerpo pueden ser circunferencias, todas ellas del mismo radio (congruentes) aunque de distinto centro. Esta situación se presenta en una noria de feria de eje horizontal, como se muestra en la figura: la armadura de la noria gira en torno al eje (rotación), pero las barquillas suspendidas de dicha armadura, prescindiendo de pequeñas oscilaciones pendulares, experimentan una traslación con trayectorias circulares.
Rotación infinitesimal
En una rotación en un ángulo infinitesimal δθ, se puede toma cos δθ ≈ 1 y sen δθ ≈ δθ, de modo que la expresión de la rotación plana pasa a ser:Si se componen dos rotaciones infinitesimales y, por ello, se descartan los términos de orden superior al primero, se comprueba que poseen la propiedad conmutativa, que no tienen las rotaciones tridimensionales finitas.
Matemáticamente el conjunto de las rotaciones infinitesimales en el espacio euclidiano forman el álgebra de Lie
 , asociada al grupo de Lie SO(3)
, asociada al grupo de Lie SO(3)Velocidad angular
Dado un sólido rígido que rota alrededor de un eje, la velocidad lineal v de una partícula se puede expresar a partir de la velocidad angular ω:Mientras que la aceleración a es:
Si el sólido rígido además de rotar alrededor de un eje tiene un movimiento adicional de traslación con velocidad instantánea V entonces las fórmulas anteriores deben substituirse por:
Dinámica de rotación
La velocidad angular de rotación está relacionada con el momento angular. Para producir una variación en el momento angular es necesario actuar sobre el sistema con fuerzas que ejerzan un momento de fuerza. La relación entre el momento de las fuerzas que actúan sobre el sólido y la aceleración angular se conoce como momento de inercia (I) y representa la inercia o resistencia del sólido a alterar su movimiento de rotación.La energía cinética de rotación se escribe:
siendo
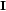 el tensor momento de inercia. La expresión del teorema del trabajo en movimientos de rotación se puede expresar así:
el tensor momento de inercia. La expresión del teorema del trabajo en movimientos de rotación se puede expresar así:de modo que, la variación de la energía cinética del sólido rígido es igual al producto escalar del momento de las fuerzas por el vector representativo del ángulo girado (
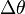 ).
).Eje de rotación
Si bien se define la rotación como un movimiento de rotación alrededor de un eje, debe tenerse presente que dicho eje de rotación puede ir cambiando su inclinación a lo largo del tiempo. Así sucede con eje de rotación terrestre y en general el eje de rotación de cualquier sólido en rotación que no presente simetría esférica. Para un planeta, o en general cualquier sólido en rotación, sobre el que no actúa un par de fuerza el momento angular se mantiene constante, aunque eso no implica que su eje de rotación sea fijo. Para una peonza simétrica, es decir, un sólido tal que dos de sus momentos de inercia principales sean iguales y el tercero diferente, el eje de rotación gira alrededor de la dirección del momento angular. Los planetas con muy buena aproximación son esferoides achatados en los polos, lo cual los convierte en una peonza simétrica, por esa razón su eje de giro experimenta una rotación conocida como precesión. La velocidad angular de precesión viene dada por el cociente entre el momento angular de rotación y el menor de los momentos de inercia del planeta:El el caso de existencia de asimetría axial el planeta es una peonza asimétrica y además el eje de giro puede realizar un movimiento de nutación.
Rotación en matemáticas
Introducción matemática
El tratamiento detallado de las rotaciones ha sido objeto de numerosos trabajos matemáticos, que abordan el problema desde diversos puntos de vista y grados de sofisticación: cuaterniones, matrices, operadores vectoriales, teoría de grupos... Todos estos enfoques son matemáticamente equivalentes y se pueden derivar unos de otros, salvo en algunos aspectos concretos y posibles resultados redundantes, y la elección de uno u otro depende del problema concreto. Con la llegada de la robótica y los gráficos informáticos, la matemática de las rotaciones ha cobrado un nuevo impulso y ha pasado a ser una materia de estudio muy activo, con particular énfasis en el enfoque basado en cuaterniones.En matemáticas las rotaciones son transformaciones lineales que conservan las normas (es decir, son isométricas) en espacios vectoriales en los que se ha definido una operación de producto interior y cuya matriz tiene la propiedad de ser ortogonal y de determinante igual a ±1. Si el determinante es +1 se llama rotación propia y si es −1, además de una rotación propia hay una inversión o reflexión y se habla de rotación impropia1 .
La conservación de la norma es equivalente a la conservación del producto interior, que se puede expresar como:
Consecuencia de ella es que las distancias y las formas también se conservan.
Como parámetro que determina la rotación se puede usar un vector (que tiene carácter deslizante) del eje de rotación y de longitud proporcional al ángulo de rotación. Sin embargo, lo normal es separar este vector en el ángulo y un vector unitario, lo que en el espacio da cuatro parámetros2 . Como consecuencia hay dos formas de representar una única rotación, pues
Rotaciones en el plano
Sea un vector A en el plano cartesiano definido por sus componentes x e y, descrito vectorialmente a través de sus componentes:La operación de rotación del punto señalado por este vector alrededor de un eje de giro puede siempre escribirse como la acción de un operador lineal (representado por una matriz) actuando sobre el vector (multiplicando al vector:
Expresión matricial
En dos dimensiones la matriz de rotación para el vector dado puede escribirse de la manera siguiente:Al hacer la aplicación del operador, es decir, al multiplicar la matriz por el vector, obtendremos un nuevo vector A' que ha sido rotado en un ángulo
 en sentido antihorario:
en sentido antihorario:siendo
Expresión mediante números complejos
Las rotaciones en el plano pueden tratarse igualmente mediante números complejos, ya que eiα es una rotación de ángulo a:El grupo de rotaciones en dos dimensiones es isomorfo al grupo de Lie, ortogonal especial SO(2) que a su vez es isomorfo al grupo unitario U(1).

Teorema de rotación de Euler
En matemáticas, el teorema de rotación de Euler dice que cualquier rotación o conjunto de rotaciones sucesivas puede expresarse siempre como una rotación alrededor de una única dirección o eje de rotación principal. De este modo, toda rotación (o conjunto de rotaciones sucesivas) en el espacio tridimensional puede ser especificada a través del eje de rotación equivalente definido vectorialmente por tres parámetros y un cuarto parámetro representativo del ángulo rotado. Generalmente se denominan a estos cuatro parámetros grados de libertad de rotación.Rotaciones en el espacio
Expresión vectorial
La expresión vectorial de las rotaciones cónicas es:donde:
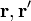 representan los vectores posición de un punto antes y después de la operación de rotación.
representan los vectores posición de un punto antes y después de la operación de rotación.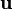 es un vector unitario que coincide con la dirección de eje de giro.
es un vector unitario que coincide con la dirección de eje de giro.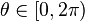 es el valor del ángulo girado.
es el valor del ángulo girado.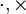 , denotan respectivamente el producto escalar y el producto vectorial.
, denotan respectivamente el producto escalar y el producto vectorial.
Expresiones matriciales
Matricialmente este producto se puede escribir de varias maneras, bien como matriz ortogonal:Donde:

La dirección principal (recta generada por un vector propio) asociaciada al autovalor 1 es precisamente el vector
 que da la dirección de eje de giro.
que da la dirección de eje de giro.Expresiones vectoriales
Se puede describir el movimiento de rotación cónica con operadores vectoriales que, al contrario que las expresiones matriciales, son independientes de las coordenadas. Así,3donde la expresión entre paréntesis funciona como operador y
 , de modo que
, de modo que 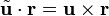 4 . Hay ciertos casos especiales de este operador:
4 . Hay ciertos casos especiales de este operador: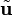 es una rotación plana de (1/2)π rad. La aplicación sucesiva de este operador da
es una rotación plana de (1/2)π rad. La aplicación sucesiva de este operador da 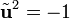 ,
, 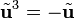 ,
,  ,
, 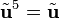 , etc., con un comportamiento parecido a la unidad imaginaria (i)5 . Es un operador hemisimétrico y en coordenadas castesianas su matriz es:
, etc., con un comportamiento parecido a la unidad imaginaria (i)5 . Es un operador hemisimétrico y en coordenadas castesianas su matriz es:
 es una rotación plana de ángulo θ. Una notación alternativa es
es una rotación plana de ángulo θ. Una notación alternativa es  (por similitud con los números complejos). La forma matricial de este
operador en los ejes cartesianos principales es particularmente
sencilla; por ejemplo, para i es:
(por similitud con los números complejos). La forma matricial de este
operador en los ejes cartesianos principales es particularmente
sencilla; por ejemplo, para i es:
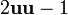 es una rotación cónica binaria (de π rad). Una rotación cónica arbitraria de ángulo θ se puede representar con dos rotaciones binarias, perpendiculares a
es una rotación cónica binaria (de π rad). Una rotación cónica arbitraria de ángulo θ se puede representar con dos rotaciones binarias, perpendiculares a 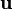 y que forman un ángulo (1/2)θ6
; la manipulación de este par de rotaciones binarias (o, de modo
equivalente, de dos reflexiones) se puede tomar como la base para la
descripción mediante los parámetros de Euler-Rodrigues. Así, el segundo de estos ejes se obtiene mediante una rotación plana del primero con
y que forman un ángulo (1/2)θ6
; la manipulación de este par de rotaciones binarias (o, de modo
equivalente, de dos reflexiones) se puede tomar como la base para la
descripción mediante los parámetros de Euler-Rodrigues. Así, el segundo de estos ejes se obtiene mediante una rotación plana del primero con 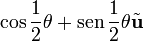 , que da los cuatro parámetros:
, que da los cuatro parámetros:

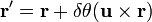
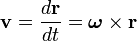
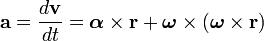

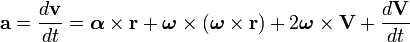

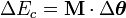

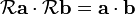


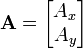
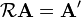
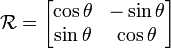
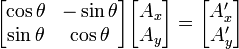
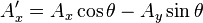
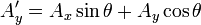
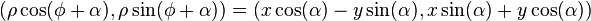


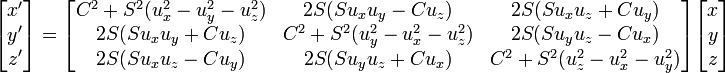


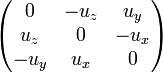
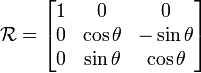
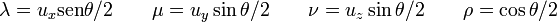
No hay comentarios:
Publicar un comentario