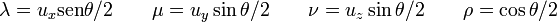fisica: 2013

lunes, 18 de noviembre de 2013

DESCRIPCION DEL MUNDO FISICO

Descartes deja a un lado la relación que tiene con el mundo sensible, pues se da cuenta que ese ser que piensa tiene sensaciones. Sin embargo, todo aquello que sentimos proviene de algo ajeno a nuestra mente. Aquellas sensaciones no pueden ser controladas por nosotros, pues dependen de algo que no es nuestro pensamiento, y éste no puede decidir entre sentir una u otra cosa. De aquí, podríamos volver a la duda hiperbólica y pensar que esto que sentimos es un Dios que nos engaña o algo parecido.

Una vez que Descartes demuestra en la primera parte de Los principios de la filosofía que Dios no puede provocar o ser causa de ningún error deja de sospechar de todo. Desaparece la duda hiperbólica de esta manera, por conducto de Dios que le da la validez para ver todo clara y distintamente en el mundo que Él ha creado. Entonces, cuando nuestros sentidos perciben clara y distintamente un cuerpo extenso con longitud, anchura y profundidad no tenemos porque dudar de su existencia, y sin temor a equivocarnos, porque para Descartes Dios no puede engañarnos, "debemos concluir que existe una substancia extensa en longitud, latitud y profundidad, que existe en el presente en el mundo con todas las propiedades que manifiestamente conocemos que le pertenecen."

Características del mundo físico

Explica Descartes que a la mente llegan ideas de forma adventicia. Estas ideas tienen una forma de garantía que implica que esa idea sea igual para todos. Por tanto, hay una sustancia y permanece al cambio, ella es la extensión. La extensión se explica que sea igual para todos porque según Descartes la medida de cualquier objeto debe ser siempre la misma y será la misma para todos. Así, limita los objetos a cosas geométricas que cuentan con largo, ancho y profundidad.

Al distinguir un cuerpo lo que nuestros sentidos perciben son sus cualidades, pero para Descartes éstas no pueden determinar la naturaleza de los cuerpos. "La naturaleza del cuerpo solamente reside en ser una substancia extensa en longitud, anchura y profundidad." La extensión no es un accidente de la substancia material, sino que la extensión es la substancia material y la única manera de entender esta substancia corpórea es por medio de su extensión Para Descartes todo lugar en el universo esta ocupado por un cuerpo. "Todo los lugares están llenos de cuerpos" Todo cuerpo que hay en el universo ocupa un lugar en él. La dimensión del lugar que ocupa el cuerpo es proporcional al espacio de este cuerpo. Es decir, no puede ser mayor o menor el lugar que ocupa, la extensión de un cuerpo y el espacio de éste es proporcional a las dimensiones del lugar, no es posible que el lugar sea más grande al espacio que ocupa el cuerpo, o bien menor. Cada lugar en el universo esta relacionado con un cuerpo y sólo con uno. Por lo tanto, es imposible que dos cuerpos compartan un mismo lugar.

imposible que dos cuerpos compartan un mismo lugar.

Para Descartes la materia es infinitamente divisible. No existe algo parecido a un átomo o una medida mínima a la que se pueda reducir la materia, sin importar que tan pequeño sea un cuerpo, éste siempre será divisible. "También es muy fácilmente cognoscible que no existen átomos o partes de los cuerpos que sean indivisible". Ésta es la naturaleza de todo cuerpo con extensión, siempre se va a poder dividir.

Recordemos que para Descartes el fundamento de su ciencia se encuentra en el pensamiento, en este sentido si uno por medio del entendimiento concibe la idea de que un cuerpo puede ser dividido en dos o más partes, y que estas partes a su vez pueden ser divididas en dos o más y estas de igual manera, hasta el infinito, es muy claro que esta idea se genera en el pensamiento. Pero, explica también que si Dios creó una medida mínima en la que se puede dividir la materia, Él por ser omnipotente tiene la posibilidad de seguirla dividiendo infinitamente, en ese sentido la materia es infinitamente divisible. "La parte extensa más pequeña que pudiera ser en el mundo siempre puede ser dividida porque tal es en razón de su naturaleza

La tierra y los cielos están formados de una misma materia; que, aunque existiera una infinidad de mundos, estarían hechos de la misma materia.

Cualquier cuerpo que se de dentro de este universo tiene estas propiedades de la extensión y la infinita divisibilidad y por lo tanto forma parte de esta materia ilimitada que no deja lugar al vacío que conforma el universo. Por lo tanto, Descartes concluye que sólo hay una materia que ocupa todo el espacio imaginable en el universo, que es ilimitado

Primera ley de la naturaleza

"Cada cosa permanece en el estado en el que está mientras que nada modifique ese estado."

Todo cuerpo que con su extensión que ocupa un espacio y se encuentra en movimiento o reposo, permanecerá en ese estado y no cambiará, hasta que una causa externa lo cambié ya sea en su extensión, espacio o movimiento. Así un cuadrado será cuadrado hasta que no haya una causa externa que lo modifique. Y si un cuerpo esta en reposo, permanecerá de esa manera hasta que una causa externa a él lo ponga en movimiento.

Segunda ley de la naturaleza

"Todo cuerpo que se mueve tiende a continuar su movimiento en línea recta."

Siguiendo la primera ley, el movimiento que describe un cuerpo después de ser cambiado por causas externas de reposo a movimiento no puede depender del azar. El movimiento se determina por leyes inmutables, así el movimiento que seguirá el cuerpo será el de un línea recta. Incluso cuando el cuerpo es forzado a mantener un movimiento circular, si éste pudiese liberarse de esa fuerza trazaría en su nuevo movimiento una línea recta.

Tercera ley de la naturaleza

"Si un cuerpo en movimiento choca con otro más fuerte que él, no pierde nada de su movimiento; ahora bien, si encuentra otro más débil y que puede mover, pierde tanto movimiento como comunica al otro

una causa externa. El cambio de estado entre reposo o movimiento que se da en los cuerpos siempre es algo externo a ellos. No puede darse el caso de que un cuerpo en reposo comience a moverse por sí mismo, o uno en movimiento se detenga por sí solo, siempre será algo externo lo que cause el cambio

20 PREGUNTAS

1. DE DONDE PROBIENE LO QUE SENTIMO

PROBIENE DE NUESTRAS MENTES

2. ¿ QUIEN DEMUESTRA LA PRIMERA PARTE DE LOS PRINCIPIOS DE LA FILOSOFIA ?

DESCARTES

3. ¿ QUE EXPLICO DESCARTES?

QUE A LA MENTE LLEGAN IDEAS DE FORMA ADVENTICIAS

4. SEGUN DESCARTES COMO DEBE SER LA MEDIDA DE UN OBJETO

DEBE SER LA MISMA PERA TODO

5. ¿ QUE PERCIBE AL DISTINGUIR UN CUERPO?

LAS CUALIDADES PERO PARA DESCARTE NO LO PUEDE PERCIVIR LA NATURALEZA

6. DONDE SE ENCUENTRA EL FUNDAMENTO DE UNA CIENCIA

EN EL PENSAMIENTO

7. DE QUE ESTA FORMADA LA TIERRA Y EL MUNDO

ESTAN FORMADAS DE UNA MISMA MATERIA

8. ¿ QUE CONCLUYE DESCARTES ?

CONCLUYE QUE SOLO HAY UNA MISMA MATERIA QUE OCUPA EL ESPACIO IMAGINABLE DEL UNIVERSO

9. COMPLETE:

TODO CUERPO QUE CON SU EXTENCION OCUPA UN ESPACIO SE ENCUENTRA EN MOVIMIENTO O REPOSO

10. VERDADERO O FALSO

El movimiento se determina por leyes inmutables

( VERDADERO)

11. SI O NO : el movimiento que seguirá el cuerpo será el de un línea recta. ( SI )

12. DE QUE ESTA FORMADA LA TIERRA Y EL CIELO

ESTAN FORMADAS DE UNA MISMA MATERIA

13. COMO SE DA EL CAMBIO DE ESTADO ENTRE REPOSO Y MOVIMIENTO.

SIEMPRE SE DAN ENTORNO A ELLO 14. SI O NO : Puede darse el caso de que un cuerpo en reposo comience a moverse por sí mismo .... (NO)

15. NO Puede darse el caso de que un cuerpo en reposo comience a moverse por sí mismo o uno en movimiento se detenga por si solo.

16. . SI O NO y por que.

Cada cosa permanece en el estado en el que está mientras que nada modifique ese estado.

si porque cada espacio se mantiene en movimiento

17.complete : Cada lugar en el universo esta relacionado con un cuerpo y solo con uno . Por lo tanto, es imposible que dos cuerpos compartan un mismo lugar.

18. si o no

DESCRIPCION DEL MUNDO FISICO deja a un lado la relación que tiene con el mundo sensible.( si )

19. DE DONDE PROBIENE LO QUE SENTIMOS

LO Q SENTIMOS PROBIENE DE ALGO DE NUESTRA MENTE

20. SI O NO: el cuerpo es forzado a mantener un movimiento circular, si éste pudiese liberarse de esa fuerza trazaría en su nuevo movimiento una línea recta. ( SI )

viernes, 15 de noviembre de 2013

MOVIMIENTO CIRCULAR Y GRAVITACIÓN UNIVERSAL

Podemos decir que el movimiento circular es aquel cuya trayectoria es una circunferencia y el módulo de la velocidad es constante, es decir, recorre arcos iguales en tiempos iguales.
VELOCIDAD ANGULAR
Veamos el siguiente gráfico que representa un objeto P describiendo un movimiento circular, desde la posición P₁ hasta la P₂, tardando un tiempo t. Si unimos las posiciones del objeto con el centro de giro obtenemos su radiovector. En la figura se aprecia cómo el ángulo girado por el radiovector al cambiar de posición el cuerpo es n. Definimos la velocidad angular como:

El ángulo se mide en Radianes (rad) y el tiempo en segundos. Por eso la velocidad angular se medirá en rad/s en el S I.

VELOCIDAD ANGULAR Y VELOCIDAD LINEAL
Sabemos que el arco s de circunferencia girado (en metros), o sea, el camino recorrido por el objeto se puede calcular multiplicando el ángulo descrito n (en radianes) por el valor del radio (en metros). Por tanto es sencillo sustituir en la expresión de la velocidad angular:

Siendo v la velocidad lineal del objeto (el espacio recorrido s entre el tiempo t que dura el movimiento). Podemos decir que:

o bien que

ACELERACIÓN NORMAL O CENTRÍPETA
El movimiento circular uniforme es un caso "especial", pues posee aceleración. Esto parece un contrasentido, ya que te preguntarás: ¿Cómo un movimiento uniforme puede tener aceleración?
Hay aceleración debido al cambio continuo de dirección del vector velocidad a lo largo de todo el movimiento.

Dicha aceleración está siempre dirigida hacia el centro, por lo que se llama aceleración centrípeta. Por otro lado, este vector puede verse que es perpendicular (o normal) al vector velocidad en todo momento. Por ello también se le denomina aceleración normal. Su módulo se obtiene dividiendo el cuadrado de la velocidad entre el radio de la trayectoria:

FRECUENCIA Y PERÍODO DEL M C U
La frecuencia f es el número de vueltas dadas en un segundo. El período T es la magnitud inversa, es decir, el tiempo (en segundos) empleado en dar una vuelta completa.

FUERZA CENTRÍPETA
Ya vimos por la segunda ley de la dinámica que toda aceleración debe ser provocada por alguna fuerza. Así pues, la fuerza centrípeta es la fuerza que origina la aceleración centrípeta. Está dirigida hacia el centro de giro y se calcula multiplicando la masa del objeto en movimiento por la a_c:

¿Serías capaz de hallar una fórmula para Fc, similar a la anterior pero en función de la velocidad angular?
¿Quién ejerce la Fc cuando giramos una piedra sujeta por una cuerda sobre nuestra cabeza? ¿Y cuando la Tierra gira alrededor del Sol? ¿Y para que la Luna describa su órbita en torno a la Tierra?
¿Cuáles son las unidades internacionales de la fuerza centrípeta y de la aceleración centrípeta?
¿Hay aceleración centrípeta en un movimiento rectilíneo?

LA POSICIÓN DE LA TIERRA EN EL UNIVERSO
Desde la antigua filosofía hasta el final de la Edad Media, el hombre había concebido dos modelos antagónicos del Universo. La teoría geocéntrica, propuesta por Ptolomeo y defendida por Aristóteles, suponía que la Tierra era el centro del Universo y colocaba en esferas concéntricas a todos los astros visibles, girando en perfectos círculos. La teoría heliocéntrica de Aristarco, perfeccionada por el astrónomo polaco Nicolás Copérnico y apoyada por el italiano Galileo Galilei en los albores de la física, a mediados del siglo XVII, señalaba al Sol como centro del sistema solar.

LAS LEYES DEL MOVIMIENTO PLANETARIO
Los estudios recopilados por el alemán Kepler que reunió muchos datos astronómicos, fundamentalmente de Tycho Brahe, le permitieron deducir tres leyes matemáticas acerca del movimiento planetario:

1ª.- Todos los planetas realizan órbitas elípticas en uno de cuyos focos está el Sol.
2ª.- La recta que une a los planetas y el Sol barre áreas iguales en tiempos iguales.
3ª.- El cuadrado del período el movimiento orbital del planeta es directamente proporcional al cubo de su distancia al Sol.

LEY DE LA GRAVITACIÓN UNIVERSAL
Su enunciado es: "La fuerza con que se atraen dos objetos es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa".
En la figura se dibuja la fuerza F que la masa M realiza sobre la masa m, situada a una distancia r de M.

Naturalmente, por la ley de acción y reacción, sobre M actuará una fuerza igual y contraria a F, que no hemos dibujado para simplificar la figura.
G es la constante de gravitación universal y vale 6,67·10^-11 N m² /kg².

Movimiento de rotación

Rotación es el movimiento de cambio de orientación de un cuerpo o un sistema de referencia de forma que una línea (llamada eje de rotación) o un punto permanece fijo.
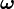La rotación de un cuerpo se representa mediante un operador que afecta a un conjunto de puntos o vectores. El movimiento rotatorio se representa mediante el vector velocidad angular $\boldsymbol\omega$ , que es un vector de carácter deslizante y situado sobre el eje de rotación. Cuando el eje pasa por el centro de masa o de gravedad se dice que el cuerpo «gira sobre sí mismo».

La rotación también puede ser oscilatoria, como en el péndulo (izquierda). Los giros son completos sólo cuando la energía es lo suficientemente alta (derecha). El gráfico superior muestra la trayectoria en el espacio fásico.

En ingeniería mecánica, se llama revolución a una rotación completa de una pieza sobre su eje (como en la unidad de revoluciones por minuto), mientras que en astronomía se usa esta misma palabra para referirse al movimiento orbital de traslación de un cuerpo alrededor de otro (como los planetas alrededor del Sol).

Concepto de rotación y revolución

La rotación de un cuerpo alrededor de un eje (exterior o interior al cuerpo) corresponde a un movimiento en el que los distintos puntos del cuerpo presentan velocidades que son proporcionales a su distancia al eje. Los puntos del cuerpo situados sobre el eje (en el caso de que éste sea interior al cuerpo) permanecen en reposo.
- La orientación del cuerpo en el espacio cambia continuamente durante la traslación.
- Un ejemplo de rotación es el de la Tierra alrededor de su propio eje de rotación, con un período de rotación de un día sidéreo.
La revolución de una partícula o de un cuerpo extenso corresponde a un movimiento de traslación del cuerpo alrededor de otro.
- Un ejemplo de revolución es el de la Tierra alrededor del Sol, con un periodo de revolución de un año.

La distinción entre rotación y revolución está asociada con la existente entre rotación y traslación de un cuerpo extenso. Si la velocidad de traslación es constante (v=cte), cada uno de los puntos del sólido recorrerá una trayectoria rectilínea con celeridad constante y todas esas trayectorias serán paralelas entre sí (movimiento de traslación uniforme). Pero, en general, la velocidad de traslación no tiene por que ser constante y la trayectoria puede ser curvilínea.
Las trayectorias recorridas por los distintos puntos del cuerpo pueden ser circunferencias, todas ellas del mismo radio (congruentes) aunque de distinto centro. Esta situación se presenta en una noria de feria de eje horizontal, como se muestra en la figura: la armadura de la noria gira en torno al eje (rotación), pero las barquillas suspendidas de dicha armadura, prescindiendo de pequeñas oscilaciones pendulares, experimentan una traslación con trayectorias circulares.

Rotación infinitesimal

En una rotación en un ángulo infinitesimal δθ, se puede toma cos δθ ≈ 1 y sen δθ ≈ δθ, de modo que la expresión de la rotación plana pasa a ser:

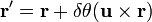
$\mathbf{r}'= \mathbf{r} + \delta\theta (\mathbf{u}\times\mathbf{r})$

Si se componen dos rotaciones infinitesimales y, por ello, se descartan los términos de orden superior al primero, se comprueba que poseen la propiedad conmutativa, que no tienen las rotaciones tridimensionales finitas.
Matemáticamente el conjunto de las rotaciones infinitesimales en el espacio euclidiano forman el álgebra de Lie $\mathfrak{so}(3)$ , asociada al grupo de Lie SO(3)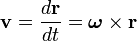

Velocidad angular

Artículo principal: Cinemática del sólido rígido

Dado un sólido rígido que rota alrededor de un eje, la velocidad lineal v de una partícula se puede expresar a partir de la velocidad angular ω:

$\mathbf{v} = \frac{d\mathbf{r}}{dt} = \boldsymbol\omega \times \mathbf{r}$

Mientras que la aceleración a es:

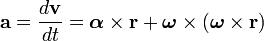
$\mathbf{a} = \frac{d\mathbf{v}}{dt} = \boldsymbol{\alpha} \times \mathbf{r} + \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r})$

Si el sólido rígido además de rotar alrededor de un eje tiene un movimiento adicional de traslación con velocidad instantánea V entonces las fórmulas anteriores deben substituirse por:

$\mathbf{v} = \frac{d\mathbf{r}}{dt} = \boldsymbol\omega \times \mathbf{r} + \mathbf{V}$

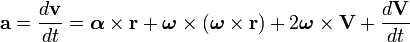
$\mathbf{a} = \frac{d\mathbf{v}}{dt} = \boldsymbol{\alpha} \times \mathbf{r} + \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r}) + 2\boldsymbol\omega \times \mathbf{V} + \frac{d\mathbf{V}}{dt}$

Dinámica de rotación

La velocidad angular de rotación está relacionada con el momento angular. Para producir una variación en el momento angular es necesario actuar sobre el sistema con fuerzas que ejerzan un momento de fuerza. La relación entre el momento de las fuerzas que actúan sobre el sólido y la aceleración angular se conoce como momento de inercia (I) y representa la inercia o resistencia del sólido a alterar su movimiento de rotación.
La energía cinética de rotación se escribe:

$E_c = \frac{1}{2} \boldsymbol\omega \cdot (\mathbf{I} \boldsymbol\omega)$

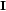siendo $\scriptstyle \mathbf{I}$ el tensor momento de inercia. La expresión del teorema del trabajo en movimientos de rotación se puede expresar así: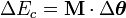

$\Delta E_c=\mathbf{M}\cdot\Delta\boldsymbol{\theta}$

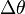de modo que, la variación de la energía cinética del sólido rígido es igual al producto escalar del momento de las fuerzas por el vector representativo del ángulo girado ( $\Delta\theta$ ).

Eje de rotación

Si bien se define la rotación como un movimiento de rotación alrededor de un eje, debe tenerse presente que dicho eje de rotación puede ir cambiando su inclinación a lo largo del tiempo. Así sucede con eje de rotación terrestre y en general el eje de rotación de cualquier sólido en rotación que no presente simetría esférica. Para un planeta, o en general cualquier sólido en rotación, sobre el que no actúa un par de fuerza el momento angular se mantiene constante, aunque eso no implica que su eje de rotación sea fijo. Para una peonza simétrica, es decir, un sólido tal que dos de sus momentos de inercia principales sean iguales y el tercero diferente, el eje de rotación gira alrededor de la dirección del momento angular. Los planetas con muy buena aproximación son esferoides achatados en los polos, lo cual los convierte en una peonza simétrica, por esa razón su eje de giro experimenta una rotación conocida como precesión. La velocidad angular de precesión viene dada por el cociente entre el momento angular de rotación y el menor de los momentos de inercia del planeta:

$\dot\phi_{prec} = \frac{L}{I_{\min}}$

El el caso de existencia de asimetría axial el planeta es una peonza asimétrica y además el eje de giro puede realizar un movimiento de nutación.

Rotación en matemáticas

Introducción matemática

El tratamiento detallado de las rotaciones ha sido objeto de numerosos trabajos matemáticos, que abordan el problema desde diversos puntos de vista y grados de sofisticación: cuaterniones, matrices, operadores vectoriales, teoría de grupos... Todos estos enfoques son matemáticamente equivalentes y se pueden derivar unos de otros, salvo en algunos aspectos concretos y posibles resultados redundantes, y la elección de uno u otro depende del problema concreto. Con la llegada de la robótica y los gráficos informáticos, la matemática de las rotaciones ha cobrado un nuevo impulso y ha pasado a ser una materia de estudio muy activo, con particular énfasis en el enfoque basado en cuaterniones.
En matemáticas las rotaciones son transformaciones lineales que conservan las normas (es decir, son isométricas) en espacios vectoriales en los que se ha definido una operación de producto interior y cuya matriz tiene la propiedad de ser ortogonal y de determinante igual a ±1. Si el determinante es +1 se llama rotación propia y si es −1, además de una rotación propia hay una inversión o reflexión y se habla de rotación impropia¹ .
La conservación de la norma es equivalente a la conservación del producto interior, que se puede expresar como:

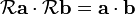
$\mathcal{R}\mathbf{a}\cdot\mathcal{R}\mathbf{b} =\mathbf{a}\cdot\mathbf{b}$

Consecuencia de ella es que las distancias y las formas también se conservan.
Como parámetro que determina la rotación se puede usar un vector (que tiene carácter deslizante) del eje de rotación y de longitud proporcional al ángulo de rotación. Sin embargo, lo normal es separar este vector en el ángulo y un vector unitario, lo que en el espacio da cuatro parámetros² . Como consecuencia hay dos formas de representar una única rotación, pues

$\mathcal{R}(\theta,\mathbf{a}) = \mathcal{R}(-\theta,-\mathbf{a})$

Rotaciones en el plano

Cambio de base o rotación de un vector.

Sea un vector A en el plano cartesiano definido por sus componentes x e y, descrito vectorialmente a través de sus componentes:

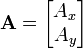
$\mathbf A=\begin{bmatrix} A_x \\ A_y \end{bmatrix}$

La operación de rotación del punto señalado por este vector alrededor de un eje de giro puede siempre escribirse como la acción de un operador lineal (representado por una matriz) actuando sobre el vector (multiplicando al vector:

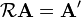
$\mathcal{R} \mathbf{A} = \mathbf{A}'$

Expresión matricial

En dos dimensiones la matriz de rotación para el vector dado puede escribirse de la manera siguiente:

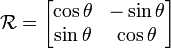
$\mathcal{R} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{bmatrix}$

Al hacer la aplicación del operador, es decir, al multiplicar la matriz por el vector, obtendremos un nuevo vector A' que ha sido rotado en un ángulo $\theta$ en sentido antihorario:

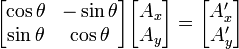
$\begin{bmatrix}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{bmatrix} \begin{bmatrix} A_x \\ A_y \end{bmatrix} = \begin{bmatrix} A'_x \\ A'_y \end{bmatrix}$

siendo

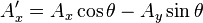
$A'_x = A_x \cos\theta - A_y\sin\theta\,$

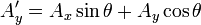
$A'_y = A_x \sin\theta + A_y\cos\theta\,$

las componentes del nuevo vector después de la rotación.

Expresión mediante números complejos

Las rotaciones en el plano pueden tratarse igualmente mediante números complejos, ya que e^iα es una rotación de ángulo a:

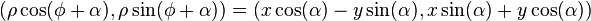
$(x,y)\in \R^2 \rightarrow x+iy = \rho e^{i\phi}\in \mathbb{C} \xrightarrow{\mathrm{rot}} z = e^{i\alpha}(\rho e^{i\phi})\rightarrow (\mathrm{Re}(z),\mathrm{Im}(z)) = (\rho\cos(\phi+\alpha),\rho\sin(\phi+\alpha))\in \R^2$ $(\rho\cos(\phi+\alpha),\rho\sin(\phi+\alpha))= (x\cos(\alpha)-y\sin(\alpha),x\sin(\alpha)+y\cos(\alpha))$

El grupo de rotaciones en dos dimensiones es isomorfo al grupo de Lie, ortogonal especial SO(2) que a su vez es isomorfo al grupo unitario U(1).

Teorema de rotación de Euler

En matemáticas, el teorema de rotación de Euler dice que cualquier rotación o conjunto de rotaciones sucesivas puede expresarse siempre como una rotación alrededor de una única dirección o eje de rotación principal. De este modo, toda rotación (o conjunto de rotaciones sucesivas) en el espacio tridimensional puede ser especificada a través del eje de rotación equivalente definido vectorialmente por tres parámetros y un cuarto parámetro representativo del ángulo rotado. Generalmente se denominan a estos cuatro parámetros grados de libertad de rotación.

Rotaciones en el espacio

Las tres rotaciones planas de los ángulos de Euler. En la primera el eje es z, que apunta hacia arriba y gira los ejes x e y; en la segunda el eje es x, que apunta hacia el frente y que inclina el eje z, y en la última de nuevo el eje es z.

Las rotaciones tridimensionales revisten especial interés práctico por corresponderse con la geometría del espacio físico en que vivimos (naturalmente siempre que se consideren regiones de escala mediana, ya que para distancias grandes la geometría no es estrictamente eunclídea). En tres dimensiones conviene distinguir entre las rotaciones planas o rectangulares, que son aquellas en las que el vector rotado y el que determina el eje de giro forman un ángulo recto, y las cónicas, en las que el ángulo entre estos vectores no es recto. Las rotaciones planas son de tratamiento matemático más simple, pues se pueden reducir al caso bidimensional descrito más arriba, mientras que las cónicas son mucho más complejas y por lo general se tratan como una combinación de rotaciones planas (especialmente los ángulos de Euler y los parámetros de Euler-Rodrigues).

Expresión vectorial

La expresión vectorial de las rotaciones cónicas es:

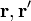$\mathbf{r}' = \mathbf{r} \cos\theta + (\mathbf{u} \times \mathbf{r})\sin\theta + \mathbf{u} (\mathbf{u} \cdot \mathbf{r}) (1 - \cos\theta)$

donde:

$\mathbf{r}, \mathbf{r}'$ representan los vectores posición de un punto antes y después de la operación de rotación.

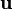$\mathbf{u}$ es un vector unitario que coincide con la dirección de eje de giro.

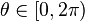$\theta\in[0,2\pi)$ es el valor del ángulo girado.

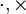$\cdot, \times$ , denotan respectivamente el producto escalar y el producto vectorial.

Expresiones matriciales

Matricialmente este producto se puede escribir de varias maneras, bien como matriz ortogonal:

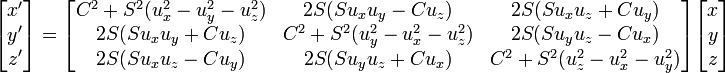
$\mathbf{r}'=\mathcal{R}_{\theta,\mathbf{u}} (\mathbf{r})\quad \Leftrightarrow \quad$ $\begin{bmatrix} x'\\ y'\\ z' \end{bmatrix} = \begin{bmatrix}C^2+S^2(u_x^2- u_y^2- u_z^2) & 2S( Su_x u_y-C u_z) & 2S(S u_x u_z + C u_y) \\ 2S(S u_x u_y+C u_z) & C^2+S^2( u_y^2- u_x^2- u_z^2) & 2S(S u_y u_z - C u_x) \\ 2S(S u_x u_z-C u_y) & 2S(S u_y u_z+C u_x) & C^2+S^2( u_z^2- u_x^2- u_y^2) \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}$

Donde:

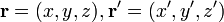
$\mathbf{r} = (x,y,z), \mathbf{r}' = (x',y',z')$

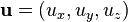
$\mathbf{u} = (u_x,u_y,u_z)$

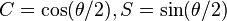
$C=\cos(\theta/2), S=\sin(\theta/2)$

Puede comprobarse con un poco de álgebra rutinaria que la matriz anterior tiene como autovalores:

$\{1, C+iS, C-iS\}= \{1, e^{i\theta}, e^{-i\theta}\}$

La dirección principal (recta generada por un vector propio) asociaciada al autovalor 1 es precisamente el vector $\scriptstyle \mathbf{u}$ que da la dirección de eje de giro.

Expresiones vectoriales

Se puede describir el movimiento de rotación cónica con operadores vectoriales que, al contrario que las expresiones matriciales, son independientes de las coordenadas. Así,³

$\mathbf{r}' = ((1 -\cos \theta)\mathbf{uu}+ \cos \theta + \mathop{\mathrm{sen}} \theta \tilde{\mathbf{u}}) \cdot \mathbf{r}$

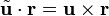
donde la expresión entre paréntesis funciona como operador y $\tilde{\mathbf{u}}= \mathbf{I}\times \mathbf{u}$ , de modo que $\tilde{\mathbf{u}}\cdot \mathbf{r}=\mathbf{u}\times\mathbf{r}$ ⁴ . Hay ciertos casos especiales de este operador:

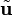$\tilde{\mathbf{u}}$ es una rotación plana de (1/2)π rad. La aplicación sucesiva de este operador da 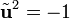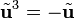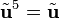$\tilde{\mathbf{u}}^2=-1$ , $\tilde{\mathbf{u}}^3=-\tilde{\mathbf{u}}$ , $\tilde{\mathbf{u}}^4=1$ , $\tilde{\mathbf{u}}^5=\tilde{\mathbf{u}}$ , etc., con un comportamiento parecido a la unidad imaginaria (i)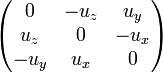⁵ . Es un operador hemisimétrico y en coordenadas castesianas su matriz es:

$\begin{pmatrix} {0} & -u_z & u_y\\ u_z & {0} & -u_x\\ -u_y & u_x &{0}\\ \end{pmatrix}$

$\cos \theta + \sin \theta \tilde{\mathbf{u}}$ es una rotación plana de ángulo θ. Una notación alternativa es $\mathrm{e}^{\tilde{\mathbf{u}}\theta}$ (por similitud con los números complejos). La forma matricial de este operador en los ejes cartesianos principales es particularmente sencilla; por ejemplo, para i es:

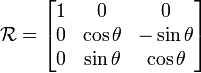
$\mathcal{R} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin\theta & \cos \theta\end{bmatrix}$

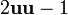$2\mathbf{uu}-1$ es una rotación cónica binaria (de π rad). Una rotación cónica arbitraria de ángulo θ se puede representar con dos rotaciones binarias, perpendiculares a 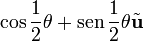$\mathbf{u}$ y que forman un ángulo (1/2)θ⁶ ; la manipulación de este par de rotaciones binarias (o, de modo equivalente, de dos reflexiones) se puede tomar como la base para la descripción mediante los parámetros de Euler-Rodrigues. Así, el segundo de estos ejes se obtiene mediante una rotación plana del primero con $\cos \frac{1}{2}\theta + \mathop{\mathrm{sen}} \frac{1}{2}\theta \tilde{\mathbf{u}}$ , que da los cuatro parámetros:

$\lambda =u_x \mathop{\mathrm{sen}} \theta/2\qquad \mu =u_y \sin \theta/2\qquad \nu=u_z \sin \theta/2\qquad \rho = \cos\theta/2$